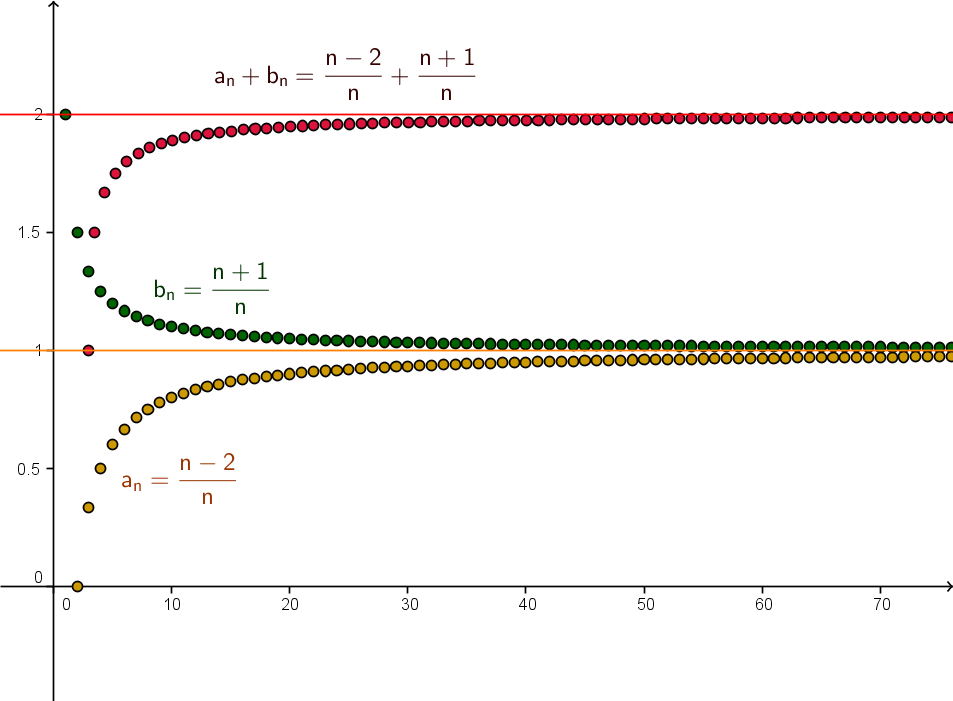
Questa successione è limitata e converge a uno. $$ \lim_{n \rightarrow ∞} \frac{n-1}{n} = 1 $$ In questo caso il limite è l=1 e a n =(n-1)/n.. Questa condizione non è verificata per ogni valore di ε>0 come richiede la definizione del limite della successione. Esempio. Per ε=1 la disequazione è soddisfatta per qualsiasi numero.. Non vale pero il contrario. Una successione limitata potrebbe non essere convergente. Ad esempio la successione (-1) n oscilla tra -1 e +1. E' limitata ma non è convergente. Nota. Se la successione converge a zero, la successione è detta successione infinitesima. E' un caso particolare di successione convergente. $$ \lim_{ n \rightarrow ∞.

Tassa di successione aumenterà? Cos’è? Chi la deve pagare e come funziona. Fedora Nadia Tamellini

SUCCESSIONE TELEMATICA esempio di compilazione dichiarazione di successione con conto corrente

LE SUCCESSIONI Si consideri la seguente sequenza di

Successione Moglie E Due Figli franciscoiko

Convergent Evolution Vs Divergent Evolution

La successione ereditaria CERTO edilizia energetica

Successioni ereditarie e successione testamentaria. Cosa dice la legge?

Proprietà delle successioni YouTube
Limiti di successione e nozioni Appunti di analisi matematica

Successione legittima guida completa e quote Avvocato Paccosi civilista Roma
Limiti

Successione Testamentaria Quote e Imposte! Che Cos'è e Cosa Prevede!

PPT LE SUCCESSIONI PowerPoint Presentation, free download ID3136130

Successione legittima guida completa e quote Avvocato Paccosi civilista Roma

Dichiarazione di successione non è accettazione dell’eredità Successione
Limiti di successione e nozioni Appunti di analisi matematica

Altri esercizi svolti sulle successioni divergenti e successioni limitate matematica & oltre

Cos'? Il Modello 240 Successione olsohaan
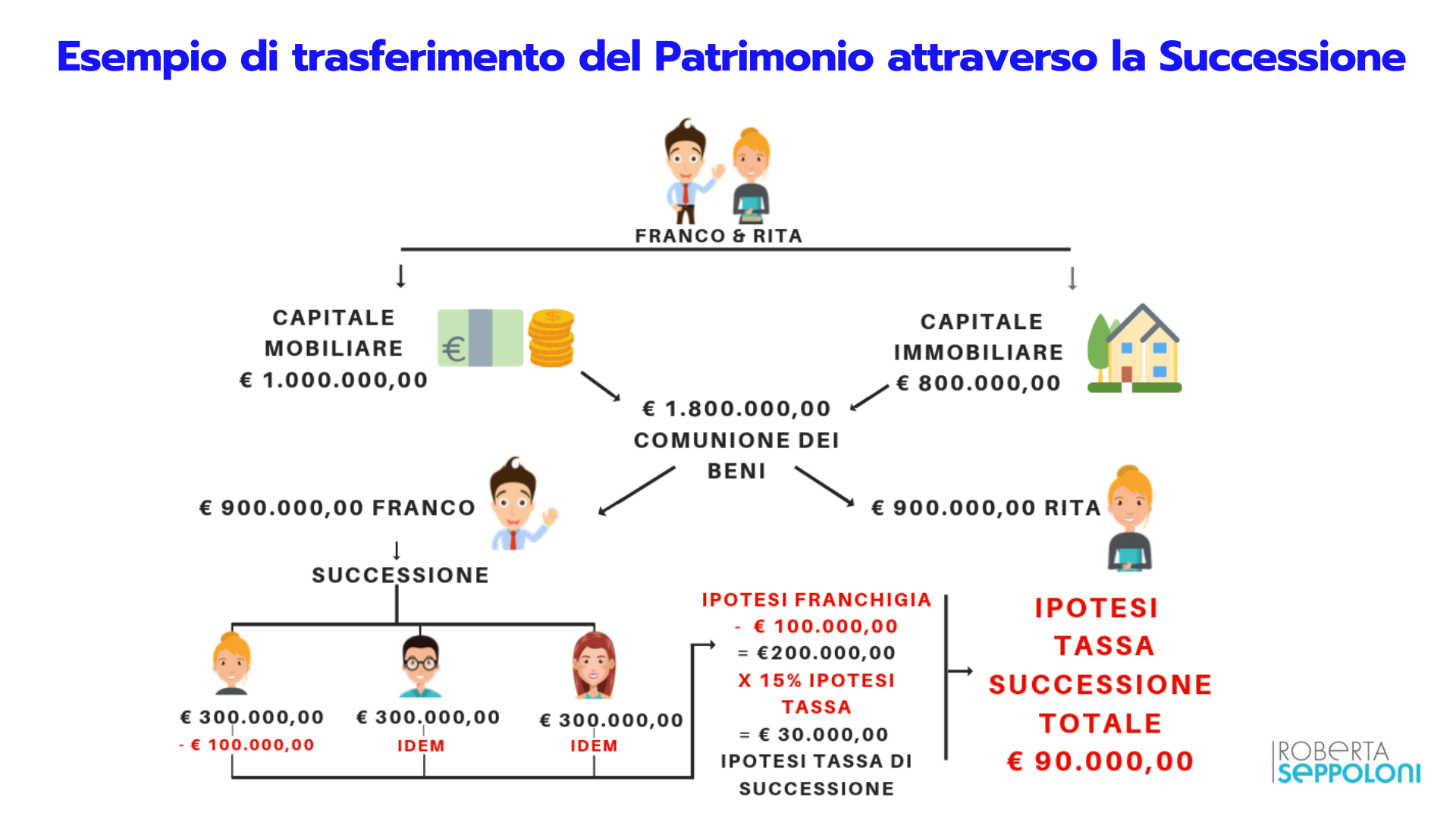
Donazioni e successioni infografica Roberta Seppoloni

La successione legittima quando si verifica?
Una successione reale (a_n)_ (n∈N) è limitata superiormente se e solo se esiste un numero reale M che sovrasta tutti i termini. Ciò si traduce formalmente in: a_n ≤ M ∀ n∈N. Esempi. 1. Ogni successione costante è superiormente limitata. 2. La successione il cui termine n-esimo è a_n = sin (n) è superiormente limitata.. Le successioni convergenti sono successioni di Cauchy. Ogni successione convergente è una successione di Cauchy.. Dimostrazione. Se la successione a n converge al limite finito l, allora per ogni ε>0 esiste un indice v tale che per ogni n>v. Per comodità ipotizzo ε=ε/2 $$ |a_n-l|<ε/2 $$ Presi due indici k,j maggiori di v, la successione è sempre convergente