Spiegelen om de y-as brengt ons naar 180˚ - 150˚ = 30˚. Omdat sin 30˚ = ½, is sin 150˚ = ½. Bereken cos 1¼π. Deze hoek ligt in kwadrant III, dus de cosinus (x-coördinaat) is negatief. Puntspiegeling brengt ons naar 1¼π - π = ¼π (45˚).. de nieuwe functie. a. y = (x + 2)³, transleren over de vector 2 3 en spiegelen in de x-as. b. y 2 x 1= − , spiegelen in de y-as, transleren over de vector 2 3. c. 1 y 3 x 2 = + +, spiegelen in de x-as en dan spiegelen in de y-as. Opdracht 8 Als je de opdrachten van dit werkblad gedaan doe dan de opdracht functies raden.

IEP groep 7 en 8 1F (basisniveau) Rekenen Meten en meetkunde Ruimtelijk inzicht Wat is

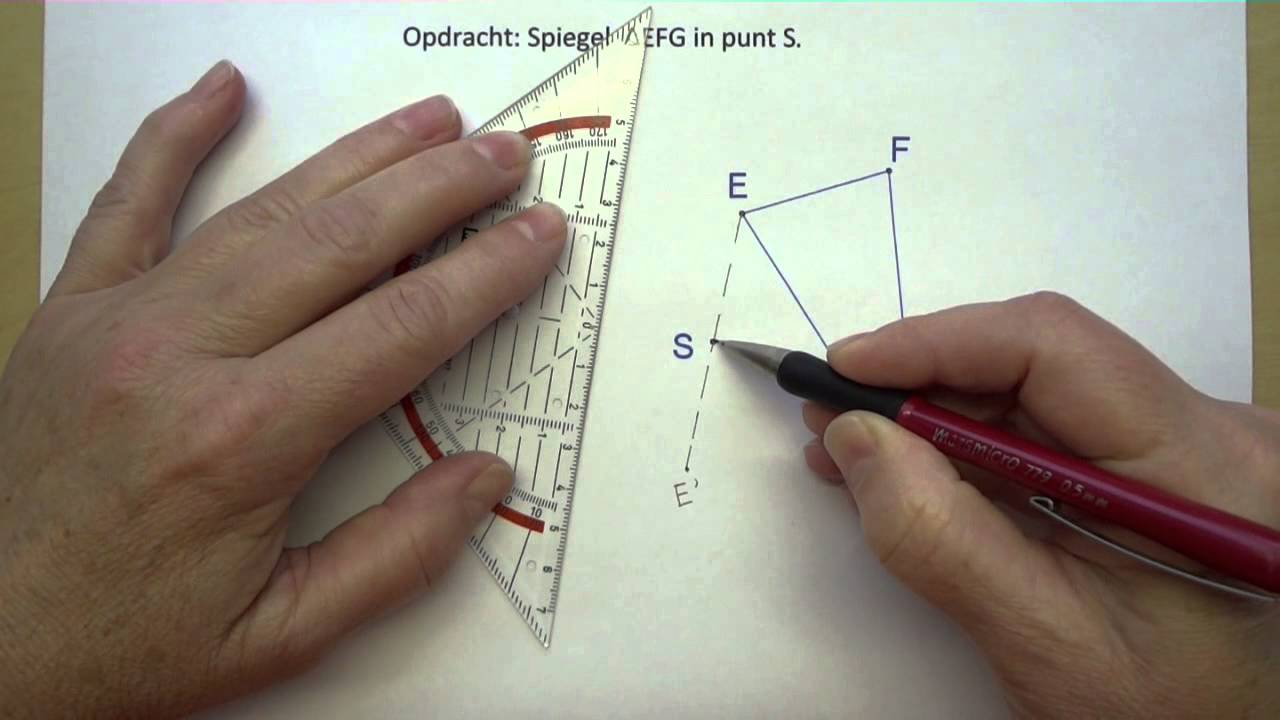
Spiegelen in een punt YouTube

Coördinaten Spiegelen in het Assenstelsel YouTube

Symmetrie spiegelen over een lijn (stappenplan) WiskundeAcademie YouTube

De spiegel De spelende wiskundeleraar

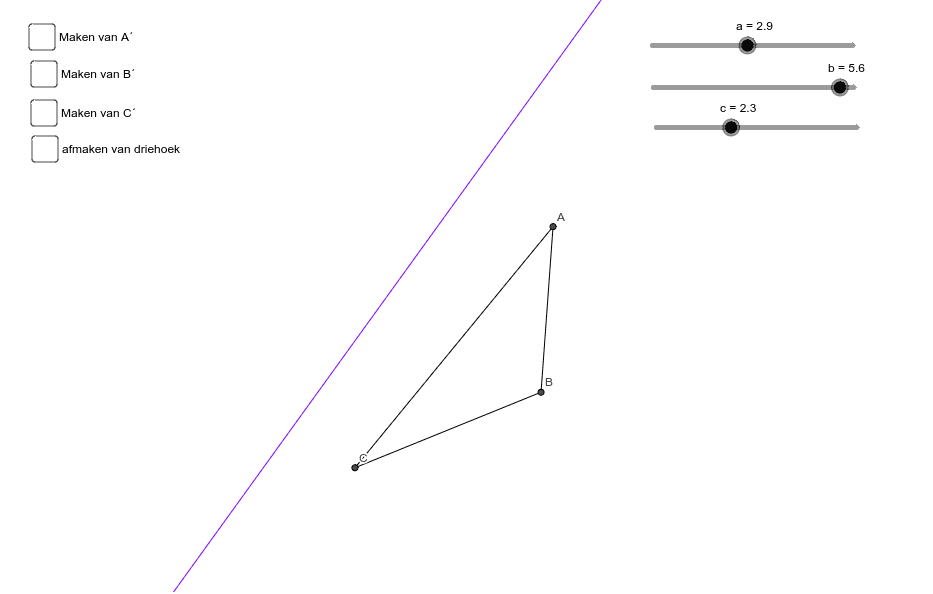
spiegelen van een driehoek in een lijn GeoGebra

Groep 1/2 Hieronymusschool groep1en2hiero

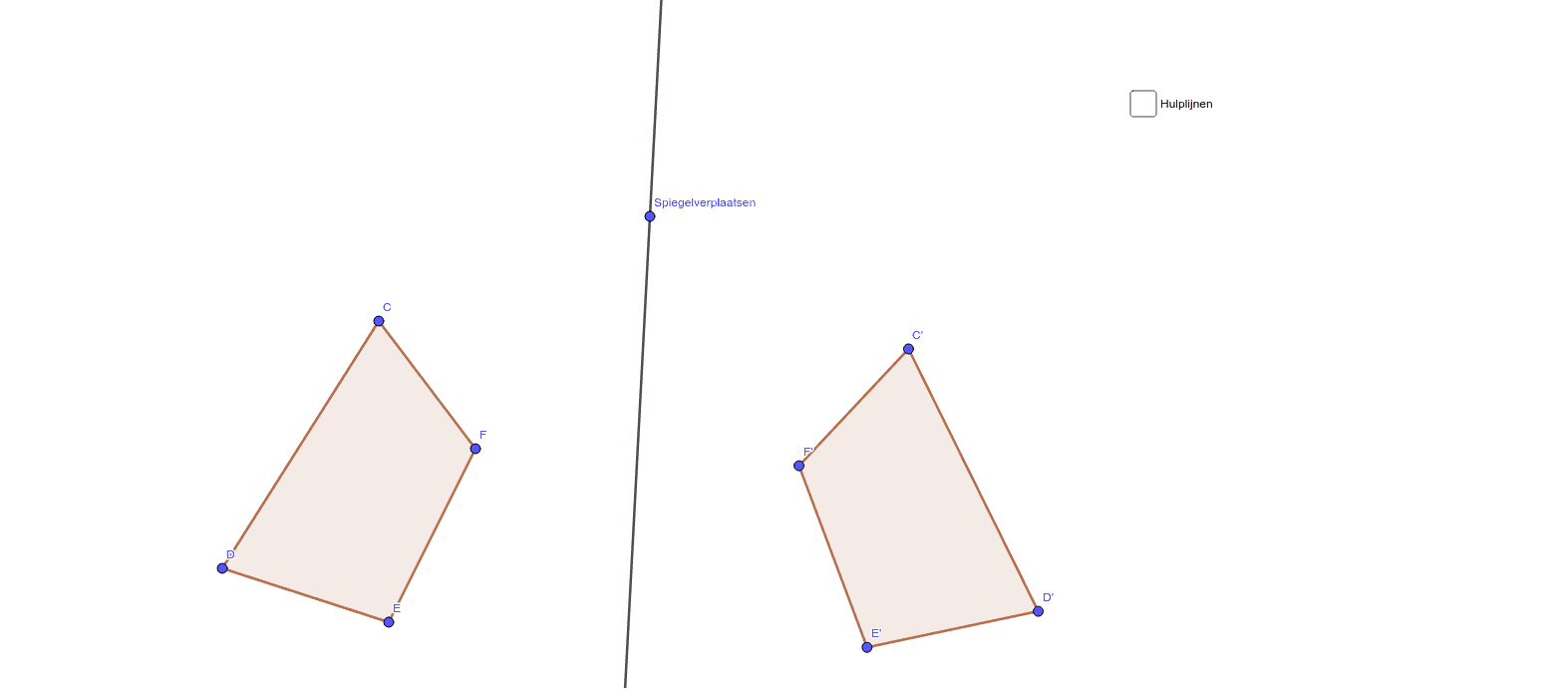
Veelhoek spiegelen GeoGebra

Spiegelen in een lijn YouTube

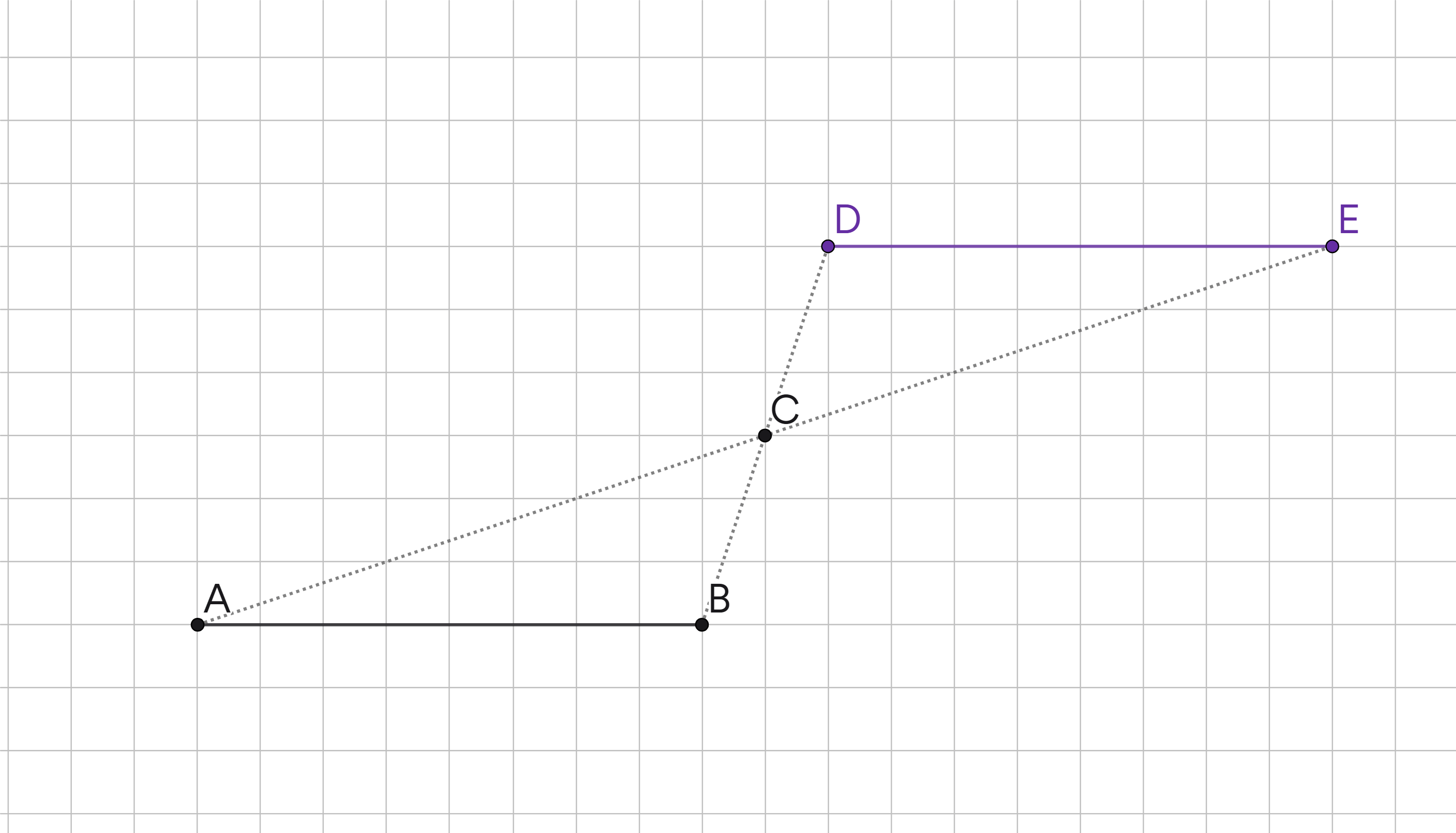
Spiegelen in een lijn en in een punt WRTS

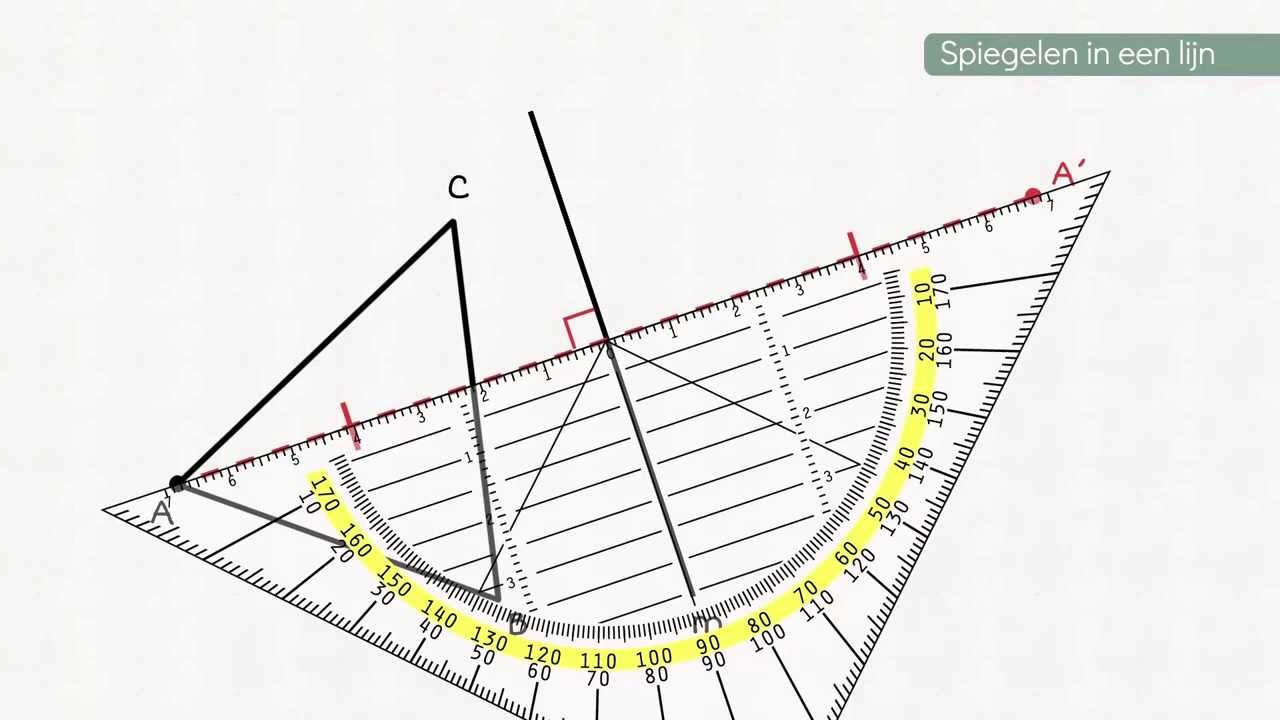
Spiegelen YouTube

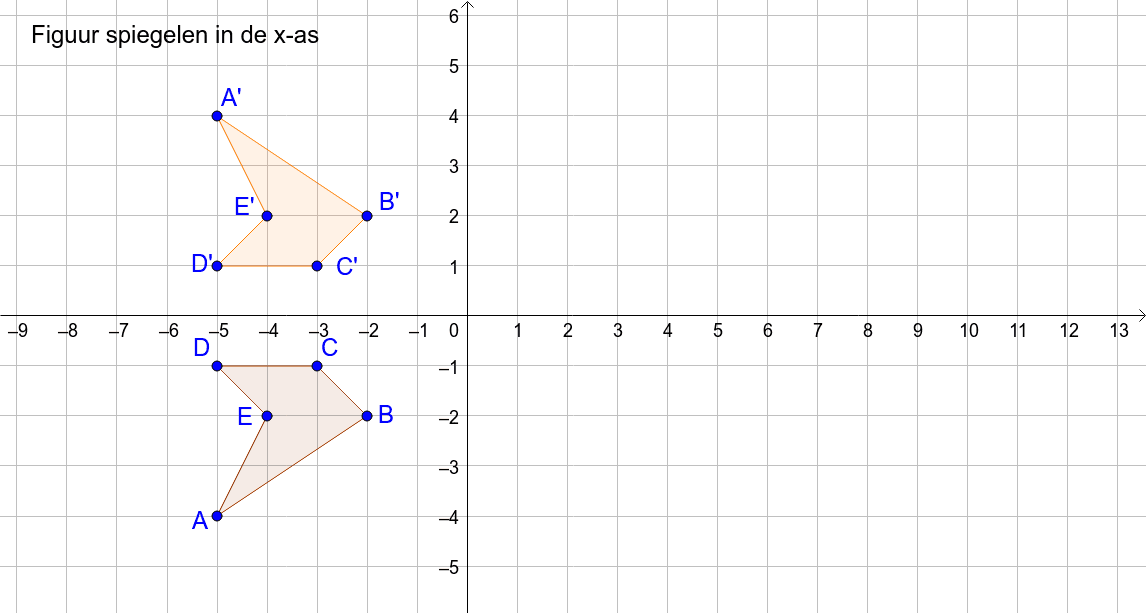
Klas 3V H30 Figuur spiegelen in de xas GeoGebra

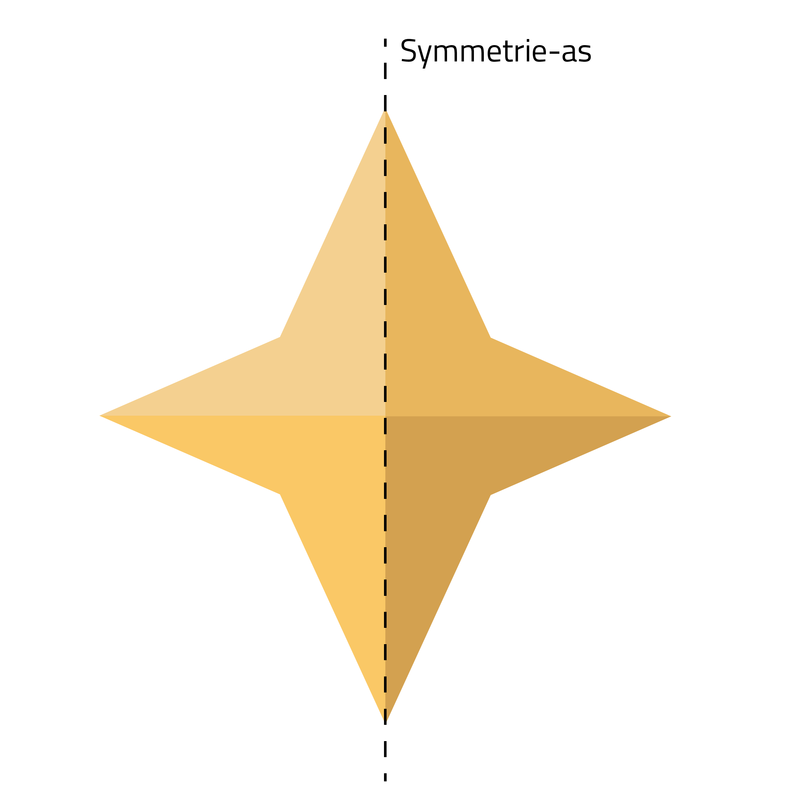
Slimleren Spiegelen in een lijn

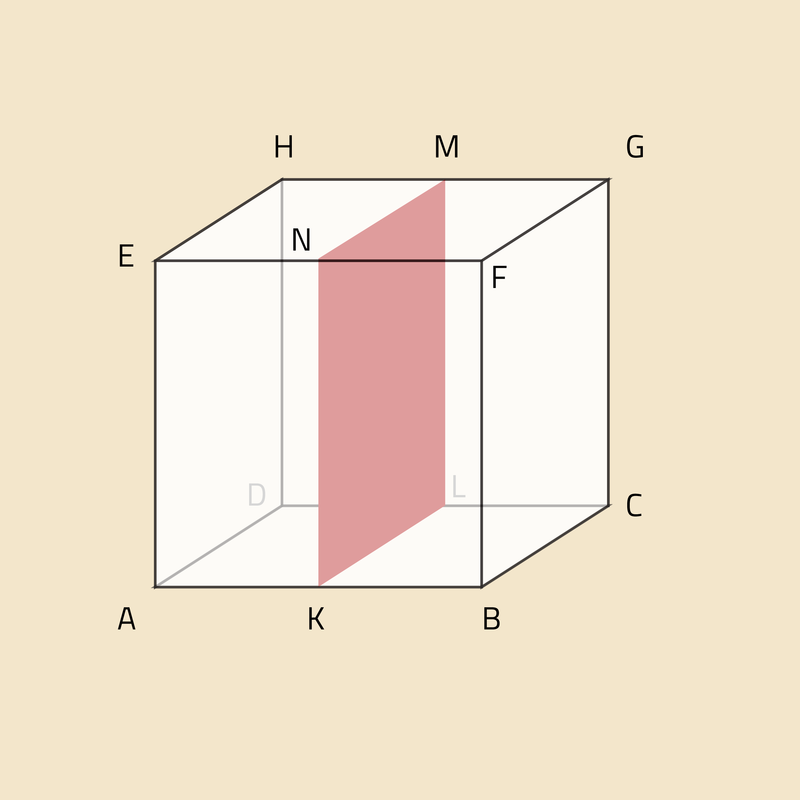
Slimleren Spiegelen in de ruimte

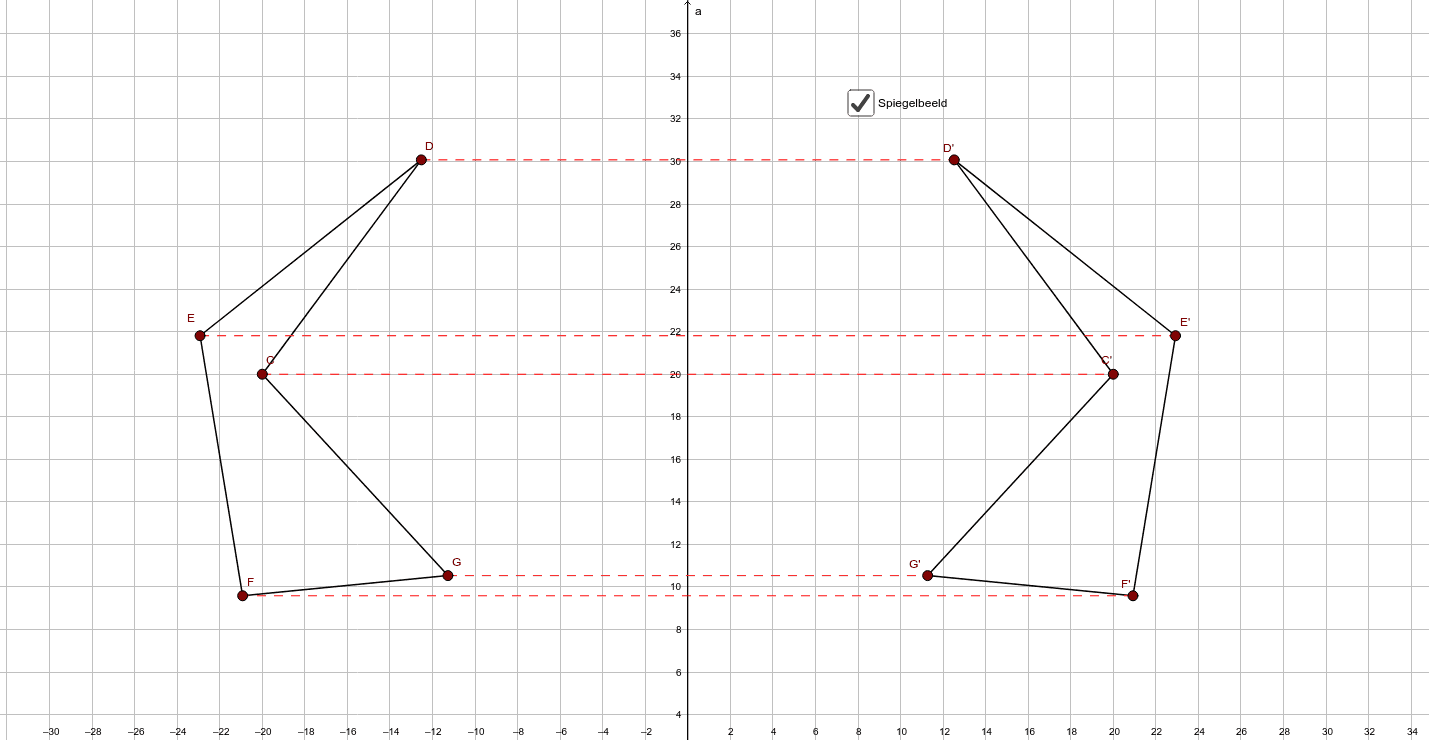
Spiegelen in de yas. GeoGebra

Spiegelen in een spiegelas YouTube

Draaien, spiegelen en verschuiven ICT in de lagere school

Spiegelingen Wiskundesite voor het secundair onderwijs

Spiegelconstructie YouTube

Spiegelen in een lijn YouTube

afstand tot de y-as 1 / a keer zo groot. 5. min voor de hele formule: spiegelen in de x-as. 6. x vervangen door -x. spiegelen in de y-as. We bekijken vijf van deze zes regels nog eens nauwkeurig, nu toegepast op een sinusgrafiek. 1. Hele formule × b. Dat geeft y = bsinx. De afstand tot de x.. Er is nog één bijzondere transformatie van de grafiek van een functie, namelijk spiegelen in de schuine lijn met vergelijking y = x y = x. Deze transformatie verwisselt de coördinaten van een punt. Deze lijnspiegeling past bij de creatie van de grafiek van een inverse functie f−1 f − 1 gegeven de inverteerbare functie f f.